Today you will…
...Examine the properties of some shapes. Your investigation will lead you to an important mathematical theorem. (This may seem a little cryptic, but saying any more than this at the outset would risk turning the tasks into a ‘guess what’s in my mind’ game!)
The learning of mathematics in school can often be procedural: facts are stated and methods are rehearsed until learners can do them well enough to pass a test. But in this approach connections are often missed and understanding can be superficial and difficult to apply to even slightly different scenarios. Working in more open-ended ways allows KS3 learners to use their natural powers to make sense of a mathematical situation and to engage more deeply with the underlying ideas. This also provides them with opportunities to learn important skills such as asking questions, making conjectures and working independently and collaboratively with other learners. In this lesson, pupils will draw tilted squares and find their areas. They will use these values to draw conclusions about the lengths of oblique lines on a square grid. This leads to a statement and proof of Pythagoras’ theorem.
Starter activity
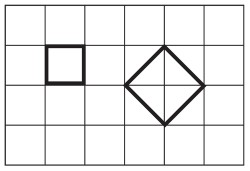
Show this image on a screen or draw it on a squared whiteboard
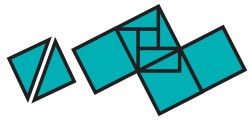
Q: What is the same and what is different about these two shapes (the ones shown in bold against the square background)? Try to identify as many things as you can.
Learners could work in pairs, compiling a list, or you could take comments from several different learners in a plenary. There is no ‘one right answer’, so try to be accepting of different ideas, especially things you hadn’t thought of yourself; give learners plenty of time. They might describe the one on the right as a rhombus (or ‘diamond’), which it is, rather than a square, which it also is. They might comment on the right angles or the number of sides. You could use this opportunity to encourage correct use of mathematical terminology. Eventually someone will say that the right-hand one is bigger, and you could ask, How much bigger? The bigger one is composed of 4 half squares, so has an area of twice as much as the left-hand one. You could follow this up by asking: How long are the sides of the squares
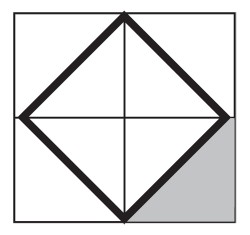
If the small one has sides of 1, because 1 × 1 = 1, then the large one must have sides of ?, where ? × ? = 2. Learners might refer to this number as ‘the square root of 2’; if they don’t, then you could do so, or alternatively you could suggest that they try to find an approximation to the number by trial and improvement on their calculators.
By focusing on the triangle shown shaded in the image above, learners will see that the longest side is the same as a side of the square, and therefore is √2 . Since this is the longest side of the triangle, it follows that √2 > 1. But the longest side of a triangle is always shorter than the sum of the other two sides (going around a corner is always further than going directly), so √2 < 1 + 1, which means that 1 < √2 < 2. This gives us an approximate position for the number √2 on the number line.
Main activities

1. Squaring up
Q: Can you make a square using this as one of the sides?
Learners may find this difficult, and might start by drawing non-square parallelograms. (You could ask: Is that a square?) They could come to the board or do it on paper. Some might think that it is impossible, but eventually someone will manage to do it. Even then, others may find it hard to copy the achievement.
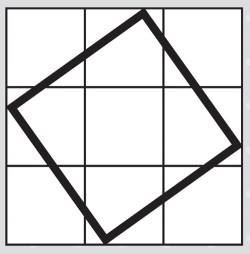
Q: Find the area of your square. You can do it however you like.
Learners might use a range of strategies – and it could be useful to organise them into groups to help them with this particular piece of problem solving. For example, they could split up the square into pieces, as in the image below, or they might break it up in some other way.
This gives an area of 5.
Q: Draw some more tilted squares and find their areas. Look for patterns. Can you draw a tilted square for every possible area?
Learners will need plenty of time if they are to produce interesting work from this starting point. In fact, it is possible only to draw tilted squares for areas that can be expressed as the sum of two squares.*
* Fermat showed that this is possible if and only if, in the prime factorisation of the number, every prime of the form 4n + 3 appears an even number of times. (See Su, Francis E., et al. ‘Sums of Two Squares’, Math Fun Facts, math.hmc.edu/funfacts.) This gives the sequence A001481 at The On-Line Encyclopedia of Integer Sequences (oeis.org/), which begins 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, ...
2. Side stepping
Q: Can you find the lengths of the sides of your squares? These will be the square roots of the areas. Learners might try to locate these on the number line in the same way as with √2 and build up a picture such as the one below. (They may also notice from this, for instance, that is 2 √5 not equal to √10 ).
3. Piecing together
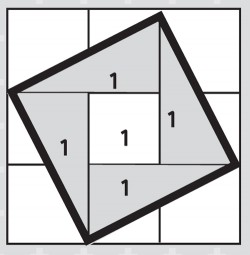
Q: Work out the areas of the pieces that make up this picture:
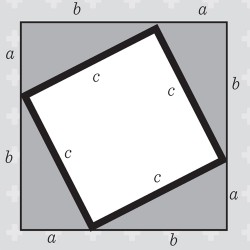
There are four triangles, each of area 1/2 ab, and a white square of area c2.
Q: What if we shuffle the pieces around, like this?
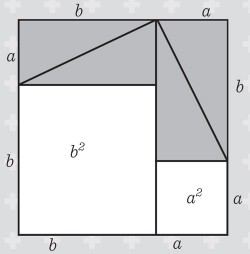
Now the grey area is the same as before, but the white area that was c2 has become a2 + b2. So a2 + b2 = c2… Pythagoras’ theorem!
Home learning
Some suggested activities for students to take out of the classroom might be:
• Find out some facts about Pythagoras. What food was he afraid of?
• Can you make a right-angled triangle where all of the sides are integers (whole numbers)?
Summary
Q: What can we say about the c-side in this triangle?
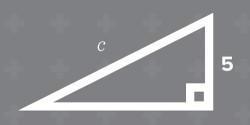
It follows from what we have done that the square of the c-side must be equal to 52 + 62 = 61, so c = 61 . Learners can go up their square numbers and ascertain that 61 is between 72 = 49 and 82 = 64, so must be between 7 and 8. (They could find a better approximation using their calculators.) They will need some time in subsequent lessons to practise finding c-sides (hypotenuses) and also adapting the method to find a-sides and b-sides (legs).
Info bar
Additional resources
• history.mcs.stand.ac.uk/Biographies/ Pythagoras.html
• maths.surrey.ac.uk/hostedsites/ R.Knott/Pythag/pythag.html
Stretch them further
• How many complete whole squares are contained in the tilted square? (Ignore part squares.) For example, there are none in the tilted square in the starter activity and there is 1 in the next tilted square shown. How does the number of complete squares depend on the particular tilted square?
• Find out what you can about irrational numbers.
About the expert
Colin Foster teaches mathematics at King Henry VIII School, Coventry (foster77.co.uk, c@foster77.co.uk)
For a huge selection of free maths lesson plans for KS3 and KS4 click here.









