Today you will…
Develop your algebra skills so that you can rearrange equations confidently. This is an important skill both within mathematics and in some other subjects.
Have you ever had a science or DT teacher sit down next to you in the staffroom and ask, “Why don’t you maths teachers teach the kids how to rearrange equations?” Of course, we do teach it, but many KS3 students seem to struggle. The process required has some similarities to that used for solving equations, yet even learners who can solve quite difficult equations sometimes get stuck with rearranging formulae. They may be able to do it when they are solving to get a number but not when they are rearranging to get a letter. So in this lesson, with the needs of the science department in mind, and an eye to cross-curricular links with English, pupils will approach this topic by beginning with some numerical work.
Starter activity
Put these sentences on the board:
1. The cat sat on the mat.
2.The mat was being sat on by the cat.
3.Sitting was taking place between the cat and the mat.
4.On the mat was sat – guess what? – the cat!
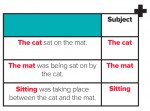
Q: What’s going on here?
Learners will comment on the sentences all saying roughly the same thing, but with different emphases. They may know the terms ‘subject’ and ‘object’ from English, and if they don’t you could explain them. The ‘subject’ is what the sentence is talking about.
In English, we can change the subject and still be saying roughly the same thing.
Write this equation on the board.
14 = 2 × 5 • 4
Q: What do you think the subject is? The subject is 14 – it’s a ‘story’ about 14 – and in mathematics the subject is still 14 if you write
2 × 5 • 4 = 14.
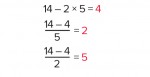
Q: Can you make one of the other numbers the subject? You still have to use all the numbers, and you can’t use any other numbers.
Learners could work on this in pairs, perhaps showing their answers on mini-whiteboards. They will probably do it by trial and error, rather than by using any particular method, checking what they are writing down by calculating. They should get:
NB Learners may need reminding of the conventions about the priority of
operations, so that 2 × 5 • 4 = 14 and
not 2 × (5 • 4), which is 18. If they try to write ‘10’ anywhere, for example, you could remind them that 10 is not one of the numbers they can use.
In mathematics, and in other subjects, such as science, it can be very useful to be able to change the subject of an equation without changing the meaning.
Main activities
Here are some suggestions for what learners could do next:
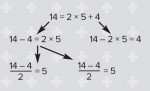
1. Linking lines
Q: With these five equations written in a tree, find operations to go along the arrows.
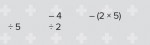
By working initially with numbers, rather than letters, learners can check at each stage that what they are writing still makes mathematical sense. They should get:
Q: Make up a different numerical equation and construct a tree for it, with operations along the branches.
Learners could do simpler or more complex ones, according to what they are comfortable with.
2. Formulating a formula
Q: What famous formulae do you know, from maths or science or anywhere else?
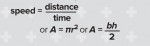
When asked this, learners nearly always say E = mc2, but they will know others too, such as for the area of a circle or triangle.
Q: Decide what steps you need to do to both sides to make each different letter the subject.
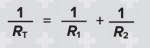
Many formulae, such as E = mc2 and A = πr2 are ‘isomorphic’ – they have the same structure – so when you know how to rearrange one, you know how to rearrange the other. Learners could look through a formula booklet to find families of formulae with the same structure; e.g.
(for resistors in parallel) matches
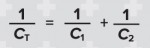
(for capacitors in series). Even if learners don’t know much about what these formulae mean, they can see that they have the same mathematical properties.
3. Understanding a ‘trick’
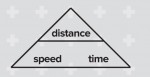
Learners may have seen mnemonics such as:

where you cover up the quantity that you require and you can ‘see’ the formula:
Mathematics teachers are not always very enthusiastic about such ‘tricks’, but learners are likely to encounter them, so it may be worth asking them to analyse why this one works, by working out what operations connect the equations.
Home learning
A suggested activity for home learning might be: Find out about some of the formulae you have rearranged today. Come next lesson ready to tell us about one of them. For instance, what is E = mc2 all about? (Anyone really interested could read Cox, B. and Forshaw, J. (2010) Why Does E = mc2? (and Why Should We Care?), Da Capo.)

Summary
Cut out the formulae right, shuffle them up, and give one to each learner. (If you have fewer learners than pieces, make sure that the ones you give out pair up!)
Q: Can you find your ‘partner’? When learners have ‘paired up’ they could sit down together and make up as many other formulae as they can that are equivalent to theirs – perhaps arranging them in a tree, with arrows connecting them, as above.
Info bar
• Additional resources many of the resources available on the web focus on procedural ‘symbol shifting’ rather than real understanding. One exception to this can be found at suffolkmaths.co.uk – click through ‘teaching materials’, ‘ks3-4 resources’, ‘algebra resources’.
• Stretch them further this is a difficult topic, which will challenge most learners. Anyone who is very confident could look at the formulae in a science formula book, such as the one at tinyurl.com/6hg7vlu and see how many they can work out how to rearrange!
About the expert
Colin Foster teaches mathematics at King Henry VIII School, Coventry, and writes books for mathematics teachers (foster77.co.uk, c@foster77.co.uk).
For a huge selection of free maths lesson plans for KS3 and KS4 click here.










