Today you will…
Find angles in triangles and use your knowledge of different kinds of numbers.
Starter activity
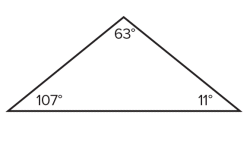
Q: Look at this drawing. Why can’t the angles be correct?
KS3 learners might say that the angles don’t look the right size; for example, the angle marked 107° should be an obtuse angle, but looks much less than 90° in the drawing. The triangle looks approximately isosceles, but the angles are all very different from each other. You could use this as an opportunity to say that any triangles we draw today are going to be sketches, so they are not intended to be accurate, and there is no point in measuring the angles with a protractor.
Q: Any other reasons?
Someone will notice that the three angles do not add up to 180°. In fact, they come to 181°. (If no one attends to this, you could ask learners to add up the angles.)
Q: Is there any way that you could tell that the angles won’t add up to 180° without actually adding them up?
Someone may notice that all three angles are odd, and because odd + odd + odd = odd then it cannot equal 180°. They might not state it as formally as this. For instance, they might comment on the fact that the sum of the units digits, 3 + 7 + 1, does not come to 10, so you could see that something was wrong without bothering to sum the tens digits. This is a similar idea.
Learners might find the idea of odd + odd + odd = odd useful later in the lesson. You may or may not want to mention this.
Main activities
Triangle numbers
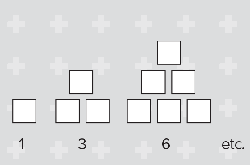
Q: We’re going to link our work on triangle angles with the triangle numbers. Who remembers what they are?
If learners haven’t encountered them recently, they may not remember them. A brief reminder should be enough to help them generate some. You could avoid saying any words and just slowly draw the following on the board (‘Stop me when you know what’s going on’).
Learners might like to draw subsequent ones on the board. Sometimes they think ‘It’s the three times table!’, but 1 is not in the three times table. In fact, the numbers are not going up in a constant amount of 3; they are going up in 1 more each time (+2, +3, +4, ... ), the number of new blocks on the bottom row.
Q: I want you to generate all the triangle numbers up to 180. (Do you think 180 will be a triangle number?)
It will be hard for learners to guess whether or not 180 is a triangle number, but this question at least raises the possibility that it might not be. Depending on your class, and how much time you have, you might or might not want them to use calculators for this.
When learners (perhaps working in groups) finish, they should compare their answers with others and resolve any disagreements. They could write the eventual list on the board:

They all need to have an accurate list for the next task.
Q: Now I want you to make up a triangle where all of the angles are triangle numbers. (What do the three angles have to add up to? [180]) This is challenging, and learners might start by making some of the angles triangle numbers. Since half the triangle numbers are even and half are odd, it might help them to bear in mind that since 180 is even they will have to do even + even + even or odd + odd + even, otherwise they won’t get an even answer. You could keep this up your sleeve and see if learners think about it for themselves before saying anything.
There are just four possible answers (ignoring the order), but give learners plenty of time to work it out for themselves. Leave the triangle numbers on the board for them to refer to. Constantly checking against this list will help learners to become more familiar with the triangle numbers. The four possibilities are: (3, 6, 171), (6, 21, 153), (15, 45, 120) and (36, 66, 78). To be sure that there are just these four will require some careful systematic thinking and checking.
Learners could produce a poster showing their ‘triangle triangles’.
Square triangles?
Q: Now I want you to try it where the angles all have to be square numbers. Do you think this is going to be easier or harder?
It’s a bit easier, as there are fewer square numbers less than 180. You may need to recap what the square numbers are, as with the triangle numbers, and make a list:

Prime triangles!
Q: Finally, we are going to try it with the prime numbers.
It would be very time consuming for learners to work all these out, so you could project the list below on the board. It would probably be easier for learners, though, if they had it on a piece of paper, as this would be more convenient to refer to:
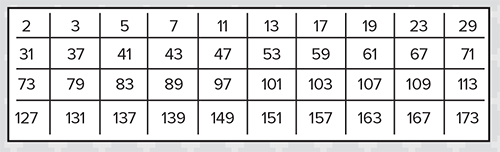
This may seem to be the most difficult, as there are 40 prime numbers less than 180. However, there is a really useful shortcut, which learners will probably not notice immediately but will become apparent as they work. Since all the prime numbers except 2 are odd, the only way to get an even answer of 180 by adding up three of them is to include 2. So every solution must have a 2° angle in it, meaning that the problem reduces to finding pairs of numbers that sum to 178, which makes it much easier. It is best to let them find this for themselves – don’t spoil it by telling them! It turns out that there are seven solutions: (2, 5, 173), (2, 11, 167), (2, 29, 149), (2, 41, 137), (2, 47, 131), (2, 71, 107) and (2, 89, 89).
Home learning
Learners could classify their triangles into different categories. Most of them will be obtuse-angled scalene, but the (36, 66, 78) triangle in the triangle numbers part is acuteangled scalene and the (2, 89, 89) triangle in the prime numbers part is acute-angled isosceles.
Summary
You could conclude the lesson with a plenary in which learners talk about which of the tasks they found easier or harder and why. What shortcuts or simplifications did they find useful?
Info bar
Stretch them further
This lesson should be challenging enough for most learners, especially if they try to justify how they know that they have found all of the solutions. But a natural extension would be to think of other kinds of numbers (e.g., cube numbers, fibonacci numbers, etc.) and make triangles based on those. Another direction to take this in would be to think of quadrilaterals, where four angles must sum to 360°. This is much harder!
Additional resources
A lovely visualisation of prime factorisations is at tinyurl.com/cosn7c3. You could project this onto the board at some point during the lesson and see how learners react. Watching it can be quite addictive! Learners might try to describe and analyse what is happening.
Another nice visualisation is at ptolemy.co.uk/primitives.
About the expert
Colin Foster is a Senior Research Fellow in the School of Education at the University of Nottingham, and writes books for mathematics teachers (www.foster77.co.uk)
For a huge selection of free maths lesson plans for KS3 and KS4 click here.








