Students often approach the topic of angles by memorising lots of vocabulary (acute, obtuse, right angle, etc.) and ‘facts’ about angles around a point, on a straight line, inside and outside a triangle and other polygons and between a transversal and parallel lines. Then they have to choose the appropriate rule to get the right answer to each calculation. In this lesson, a clock face is used to stimulate some calculations involving angles. First, KS3 students are invited to estimate the size of the angle and then to calculate it exactly. Initially, some of the calculations are quite easy, while others are more complicated as the lesson progresses. Provided that students know that there are 360° in a whole turn, they should be able to work out everything else for themselves.
WHY TEACH THIS?
Calculating angles often involves following rules based on ‘angle facts’ that are poorly understood. In this lesson, students are encouraged to use their intuition to estimate and then calculate the sizes of angles on a clock face.
STARTER ACTIVITY
If you have an analogue clock on the wall in the classroom, you might want to remove it before this lesson – or, alternatively, make use of it to support students’ visualisation.
Q. I want you to imagine an ordinary clock with an hour hand and a minute hand. Can you tell me a time when the angle between the hands is 90°?
Students will probably say 9:00 or 3:00, which are both correct, but they might also say other times which are only approximately correct, such as 9:30 or 6:15. One way to deal with this is to divide the board into two sections (without labelling them) and write exact answers in one section and approximate answers in the other. Keep going until you have some times in each section.
Q. Why do you think I have put these times here and these times here? Can you think of any more times that would go with these ones? Or with these ones?
If students don’t see the difference, ask someone to come to the board and draw exactly where the hands are at one of the times, such as 9:30, which is in the approximate section of the board. The student will probably draw something like
I
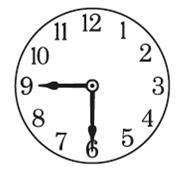
and you can ask other students whether they agree.
Q. Is that exactly right? If students still don’t see the point, then they may need to examine a real clock. They will realise that the hour hand doesn’t jump suddenly from 9 to 10 but moves smoothly, so that at 9:30 it will be half way between 9 and 10.

Q. Can you estimate the size of the angle? Students might be able to work it out exactly, but even if not they should be able to see that it is a bit more than 90°.
Q. Which of the times are exactly 90° and which are a bit more? Are any less than 90°?
Students might be able to visualise the pictures in their heads or they may need to do some sketches to work out which are which.
Q. Can you make up some more times that are just a bit more than 90° and some that are just a bit less?
Times such as 10:05, 11:10, 12:15, 1:20 and 2:25 are all a bit less than 90°, whereas times such as 4:05, 5:10, 6:15, 7:20 and 8:25 are all a bit more than 90°.
MAIN ACTIVITIES
Q. Can you calculate the angle between the hands at 9:30 exactly?
You could clarify that by “the angle” you mean the smaller angle, not the reflex angle around the back of the two hands, but students will probably assume this.
Students could work on this in pairs.
Q. What answer did you get and how did you work it out?
Encourage students to explain their different methods. They may realise that because there are 12 numbers around the clock face the angle between each adjacent pair will be 360/12= 30°. So at 9:30 we have 3½ of these, which is 3½ × 30 = 105°. Alternatively, they might say that the angle is 90° plus half of 30°.
Q. I want you to work out the angles for some of the other different times on the board and for other times where the hands are close to 90°.
You could specify how many different times you want students to calculate the angles for.
Students who are very confident with this could try difficult times, like 1:25 (the answer is 107.5°). Students who find it difficult to begin could start with times that are on the hour, such as 10:00, or times that are on the half hour, such as 3:30.
Remind the students that they need to be able to explain how they calculated their answers and convince everyone that their answers are correct. It is useful to encourage them to estimate the sizes of their answers before they start and to make sure that their final answers are sensible.
Watch out for students assuming that the hour hand is always pointing directly at the number, or assuming that if it is in between then it is always half way between. It is also useful when checking answers to realise that the angle for a time that is any whole number of minutes will be a multiple of ½°, because 360/ 12x60= 0.5°, so there should not be any answers like 135.3777°. (A spreadsheet for calculating the angles is given in the “Additional resources” section.)
STRETCH THEM FURTHER
Can you find a time where the hands lie in a straight line (i.e., make 180° with each other)? The only easy exact answer is 6:00. However, since the hands turn smoothly it will happen another 11 times over the next 12 hours. Since the intervals will be equally spaced, the hands will lie in a straight line every 1 1/11 hours; i.e., at about 7:05:27, 8:10:54, 9:16:22, etc. With similar reasoning students can tackle questions like:
- At what times will the hands point in exactly the same direction?
- At what times will the hands make exactly a right angle?
Confident students could look for times where the hands make a trickier angle, such as 100°, or pose additional questions relating to the second hand (which, of course, is actually the ‘third’ hand!).
DISCUSSION
You could conclude the lesson with a plenary in which the students talk about the times that they have chosen and the angles that they have worked out. Sometimes two groups will have worked on the same time, and they may have used different methods, which could be interesting to discuss.
Q. Can someone tell us a time that they tried that was quite easy to calculate? What answer did you get? Does that seem about the right size to everyone else? Can you show us how you worked it out?
Q. Can someone tell us a time that they did that was a bit harder than that one? How did you work yours out?
Q. Did anyone try an even more difficult time than that one? How did you do yours?
Q. What ways of working these out did you find useful? Did you find any quick ways or shortcuts? Did you notice anything interesting?
The times listed earlier have the following angles:
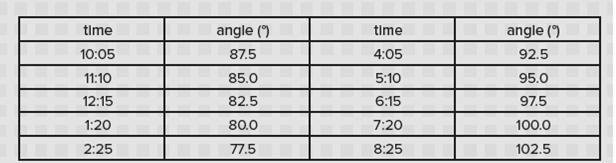
Students could think about patterns they notice, such as why in the first list the angles go down in 2.5°s, whereas the second list they go up in 2.5°s. In the first list, every time we move on 65 minutes the minute hand will be 30° further round but the hour hand will move 30° plus 1/12 of 30°, which is 2.5°, so this is how much the total angle will decrease by each time.
ABOUT OUR EXPERT
Colin Foster is an Assistant Professor in mathematics education in the School of Education at the University of Nottingham. He has written many books and articles for mathematics teachers (see www.foster77.co.uk).
For a huge selection of free maths lesson plans for KS3 and KS4 click here.









