When learners are bored in maths lessons they sometimes ask, “When will we ever actually use this?” But even topics that are unlikely to feature in everyday life can still be fun for learners to work on if they experience them as a puzzle to solve, says Colin Foster…
Today you will…
Practise solving quadratic equations by factorising while working on a deeper problem
How can KS4 learners become confident and fluent with techniques such as factorising quadratics without simply ploughing through pages of exercises? One way is to offer a scenario in which they need to construct their own quadratic equations in order to solve a bigger problem. Lots of practice happens along the way, while something a bit more interesting is going on.
Starter activity
Q: Do you remember how to solve a quadratic equation like:
x2 - 7x - 30 = 0
The easiest way is to factorise the left-hand side
(x + 3)(x - 10) = 0
(The 3 and the –10 come from the fact that their sum is –7, the coefficient of x, and their product is –30, the constant term.)
Now if two numbers multiply to make zero, either the first one is zero or the second one is zero. So in this case, either x + 3 = 0 or x – 10 = 0, giving the two answers x = –3 or 10.
Q: What if I change the starting equation by sticking a ‘2’ on the front:
2x2 – 7x – 30 = 0 ?
You can still solve it by factorising, but the factorising is harder now because the lefthand side is non-monic (i.e., the coefficient of x2 is not 1). Sometimes learners do this by trial and error, but a more systematic method is to place x’s in two brackets and write the coefficient of x (which is 2, here) three times:
Then put in two numbers that have a sum of –7 (the coefficient of x, as before), but this time they need to have a product of 2 × (–30) = –60, the product of the coefficient of x 2 and the constant term. The two numbers required here are 5 and –12, so you get:
which simplifies to (2x + 5)(x – 6).
There are other perfectly good ways of factorising non-monic quadratics, but this is a method learners (or even teachers) may not have seen [Note 1, below].
So (2x + 5)(x – 6) = 0, meaning that either 2x + 5 = 0 or x – 6 = 0, giving x = –2.5 or 6.
Learners could try solving x2 + 17x + 30 = 0 and 2x2 + 17x + 30 = 0 to see if they can do them themselves. (The answers are x = –15 or –2 and x = –2.5 or 3, respectively.)
Main activities
1. Connected quadratics
Q: Along each side of the triangle, make the two quadratic expressions equal and solve the equation.
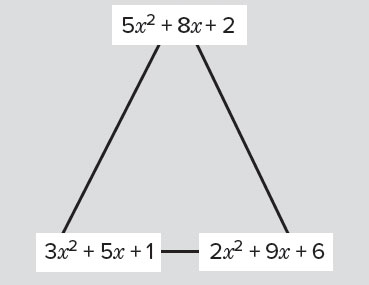
This triangle of expressions leads to three equations, all of which can be solved by factorising. The equation formed along the bottom side of the triangle is monic, so learners could start with that one, as it is the easiest; the other two are non-monic. Learners could write their solutions along the sides of the triangle:
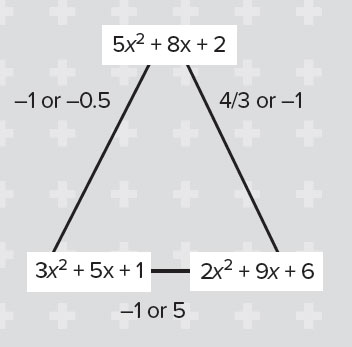
2 Make up your own
Q: See if you can make up your own triangle of connected quadratics. Remember, all three equations must be solvable by factorising!
This is quite hard and will engage learners in a lot of useful trial and improvement practice at solving quadratics (or trying to!) They will realise the important fact that not all quadratics have real solutions, and even those that do cannot necessarily be solved by factorising.
Additional (harder) challenges could be:
Q: Can you make all the solutions integers?
Q: Can you make a square of connected quadratics, forming four equations, each of which can be solved by factorising?
Q: Can you make a square of connected quadratics, including the diagonals, so that there are six equations, each of which can be solved by factorising?
3 Poster explanations
Learners might like to design a clear and attractive poster to illustrate how to solve quadratic equations by factorising. They could tackle monic or non-monic cases, or both.
Summary
You could conclude the lesson with a plenary in which learners share their creations and show the different expressions that they have constructed. How did they go about it? What problems did they encounter? Could they explain to someone else how to do it?
Home learning
Learners could try to construct a triangle in which one of the expressions is quadratic and the other two are linear (i.e., so-many lots of x, plus or minus a number; no x2 term). This should lead to two quadratic equations and one linear equation, all of which should give integer answers.
Stretch them further
The lesson began with the factorisable expression x2 – 7x – 30, which was also factorisable when a ‘2’ was added on the front to give 2x2 – 7x – 30. Learners might like to try to find other monic quadratics which are factorisable both before and after sticking a ‘2’ (or perhaps some other integer) on the front. You can find out more about this at Foster, C. (2012) Quadratic Doublets, Mathematical Gazette, 96(30), 264–266.
Additional resources
A really nice resource, particularly for use on an electronic whiteboard, is tinyurl.com/cbyw4yx there are some suggestions about ways of using it at tinyurl.com/czuuglu, but the basic idea is for learners to conjecture about the contents of the cells in the grid, based on their awareness of the structure, as other cells are revealed. each cell contains a quadratic expression in both factorised and expanded form.
About the expert
Colin Foster is a Senior Research Fellow in the School of Education at the University of Nottingham, and writes books for mathematics teachers (www.foster77.co.uk)
For a huge selection of free maths lesson plans for KS3 and KS4 click here.











When learners are bored in maths lessons they sometimes ask, “When will we ever actually use this?” But even topics that are unlikely to feature in everyday life can still be fun for learners to…