Today you will…
Learn about factors and multiples that numbers have in common with each other.
Sometimes KS4 learners encounter the ideas of highest common factor (HCF) and lowest common multiple (LCM) as procedures to follow to obtain answers, without much sense of what these quantities represent or why the procedures work. This lesson builds up to having learners find numbers to fit a specified HCF and LCM, giving them an opportunity to explore what possibilities are allowed by these constraints. The trial and error involved also gives plenty of practice at the techniques.

Starter activity
Put these Questions to Think About on the board as (or before, if possible) learners enter the room. Some learners may start talking about them as they get seated, but it doesn’t matter if they don’t
• What is a factor? (For example, 2 is a factor of 6.)
• Does every number have factors?
• Can you think of a number that has… exactly 2 factors? ... exactly 3 factors? ... exactly 4 factors?
When everyone is settled, you could ask:
Q: Does anyone have any comments on, questions about or answers to any of these? You can start with whichever one you want.
A factor is a number (a positive integer) that goes into another number. The ‘goes into’ aspect has sometimes led people to call them ‘guzintas’, which can be fun (see http://tinyurl.com/cgavys3), but learners need to know that the proper mathematical name is ‘factor’.
Every number has at least 1 factor, because 1 is a factor of every number. The only number with exactly 1 factor is 1, and all prime numbers have exactly 2 factors, which learners might realise. Numbers with an odd number of factors are always square numbers; in particular, numbers with exactly 3 factors are the squares of prime numbers. For example, 25 has 3 factors, because it is the square of 5, which is prime. There are two possibilities for numbers with 4 factors: either they are semi-primes (the product of two different prime numbers), such as 6, which is 2 x 3, or the cube of a prime number, such as 8, which is 23.
Main activities
1. Finding numbers with different numbers of factors
If learners seem quite interested in the starter activity, then you could develop it into an investigation, where they try to find numbers with 5, 6, 7 factors, etc. It could be a good way of practising finding factors. Either they could take the numbers in order and see how many factors each one has, and look for patterns, or they could explore products and powers of primes and then see how many factors the numbers that they have created have.
2. Common factors
Q: Two is a very common factor – it goes into lots of numbers. What numbers have 2 as a factor?
Learners might list some, but the general answer is the even numbers.
Q: The most common factor of all is 1, which goes into every number. What are all the factors that 12 and 20 have in common?
One way to answer this is to list the factors for each number:
12: 1, 2, 3, 4, 6, 12
20: 1, 2, 4, 5, 10, 20
The factors in common (common factors) are 1, 2 and 4.
Q: The lowest common factor of every pair of numbers is 1. That isn’t very interesting. The highest common factor (HCF) here is 4. When might an HCF be important?
One situation that learners might think of is when cancelling down fractions. If you want to simplify 12/20, you could divide the numerator and denominator by any common factor (e.g., 2), but dividing by the highest common factor (HCF) of 4 simplifies the fraction as much as possible in one go, giving 3/5.
Give each group of learners a table of numbers like this.
Q: We can fill in the HCF of 12 and 20 by putting a 4 in that cell. In groups, try to complete the table.
Learners may notice that, because of the line of symmetry along the leading diagonal, it is possible to put 4 in the other (12, 20) cell as well, so you might agree to complete just the lower diagonal half of the table. By working in groups, and noticing patterns as they go, learners will be able to complete the table reasonably quickly – they need not be intimidated by the number of cells!
Instead of putting 1 when the numbers are co-prime (e.g., 6 and 13), learners might think that ‘there isn’t one’, but since 1 goes into every number, every pair of numbers will have an HCF, so there should be some 1s in the table.
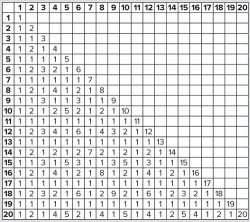
There are many patterns here that learners could highlight in colour and comment on. Finding reasons for the patterns that they see could extend their appreciation of number.
3. Constructing LCM
Q: You now know what a highest common factor is. What do you think a lowest common multiple is?
Learners should be able to
construct by analogy a meaning
for lowest common multiple (LCM).
It is the smallest value which both
of the given numbers go into.
Another phrasing is that it is the
smallest number that is in both
times tables. So the LCM of 6 and
8 can be found by writing the first
few multiples of each number:
6: 6, 12, 18, 24, 30, 36, …
8: 8, 16, 24, 32, 40, 48, …
So the LCM is 24.
Sometimes learners think that the LCM is just the product of the two numbers (48 here), and a good way to deal with this misconception is to ask them to work out when that is true. The answer is that it is true when the numbers are co-prime (i.e., have an HCF of 1). In general, HCF x LCM = product of the two numbers.

4. Make up HCF/LCM puzzles
Q: Think of two numbers. Work out their HCF and their LCM. Now tell someone else the HCF and the LCM that you have worked out. Can they find what your two numbers were?
This is an interesting investigation for learners, because sometimes there will be more than one possible answer and sometimes there won’t. Sometimes telling someone else the HCF and LCM is sufficient information for them to find the original numbers, and sometimes it isn’t. For example, if I tell you that my HCF is 6 and my LCM is 60, my numbers could have been 12 and 30, but they could also have been 6 and 60. Learners could explore when there are multiple solutions. Dealing with HCF and LCM together is a good way to work on possible confusions between the two quantities.
Home learning
Two suggested activities for home learning might be:
• Look back through your maths work and try to find an ‘application’ (i.e., a use or a context) for LCM. One situation is finding common denominators when adding or subtracting fractions. The phrase ‘lowest common denominator’ has even entered ordinary English language, and learners could try to explain what it means.
• Find the number less than 1000 which has the most factors. Learners (even teachers!) may be surprised that the answer is 840.
Summary
If there is time (or in a subsequent lesson), learners could make posters summarising, with examples, the meanings of HCF and LCM. Otherwise, you could have a shorter plenary in which learners do this orally, perhaps sharing some of the puzzles they have made up and their solutions.
Info Bar
Additional resources
A useful tool for prime factorising is at http://tinyurl.com/bosf2vm and a tool for practising these ideas is at hyperlink http://tinyurl.com/cs92lu
Stretch them further
Working out the HCF and LCM of three numbers, rather than just two, is a good way to extend these tasks. Making up HCF/LCM puzzles in which three numbers have to be found, and finding all their possible solutions, can be interesting for learners who are confident with using two numbers.
About the expert
Colin Foster is a senior research fellow in the School of Education at the University of Nottingham, and writes books for mathematics teachers www.foster77.co.uk
For a huge selection of free maths lesson plans for KS3 and KS4 click here.