Rich mathematical tasks, with lots of potential outcomes, can present all learners with engaging and worthwhile challenges, says Colin Foster…
In mathematics, short, closed tasks often require a lot of careful differentiation if all learners are to benefit equally from them. On the other hand, richer, more open-ended challenges can offer everybody (perhaps even the teacher) appropriate mathematical experiences. In this lesson, learners explore a sequence of gradually larger shapes and consider what mathematical questions they can ask about them.
STARTER ACTIVITY
Have a look at these shapes. They are not drawn accurately. What is the same and what is different about them?
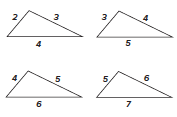
There are lots of things that learners might say. All of the shapes are triangles and they all have numbers written on the sides, which are their lengths. There are no units, because this is a pure maths problem, but you could put ‘cm’ or something after each number if you think that that would help. All of the triangles look exactly the same, and learners might be puzzled by the idea that they are mathematical sketches and are not intended to be accurate drawings. They need to get used to this, as ‘not drawn accurately’ often appears beside diagrams on examination papers! Once learners accept that the triangles represented by these sketches are not identical, there are many similarities and differences that n The areas are getting bigger from left to right.
- The shapes are not mathematically similar.
- The top angle in the triangle is getting bigger from left to right.
- The side lengths are always consecutive numbers
- The bottom side gets 1 bigger each time (as do the other sides).
It doesn’t matter if learners say things that are wrong at this stage, as these things can be addressed in the rest of the lesson. For example, they might think that the triangles are all mathematically similar because their sides are the same amount bigger each time. Once a number of observations have been made, you could ask:
Q: What mathematical questions can you ask about this?
It can be useful to write on the board the suggestions offered, whether you think they are ‘good’ ones or not. At the end, learners can select an enquiry that they want to work on. You can always add in some ideas of your own if there are particular things that you want to cover. It takes time for learners to get good at posing mathematical queries. If suggestions are not forthcoming, remind them of some of their initial observations and ask them whether they can turn any of these into questions. Some possible examples are mentioned on the next page, but it would be good to go with whatever comes up.
MAIN ACTIVITIES
What do these triangles look like when drawn accurately? Learners could use compasses or a dynamic geometry package that they are familiar with (e.g., the free software Geogebra geogebra.org) to construct these triangles accurately. They could then return to the initial question about what is the same and what is different about them, now that they can look at them drawn precisely. For example, learners might categorise them as: (Some learners might recognise the 3-4-5 Pythagorean triple, and know that it is going to be a right-angled triangle before they draw it.) Learners could measure the angles in each triangle and look for patterns in the answers (see below).
What are the ‘other’ triangles in this sequence like?
Learners might wonder where the (1, 2, 3) triangle is, that would logically come first. In fact, you cannot have a triangle with sides 1, 2 and 3, and learners who try to construct it accurately will discover why. They could explore other ‘impossible triangles’ and generalise what they find to the triangle identity, which says that if a ≤ b ≤ c are the three sides of a (possible) triangle, then a + b > c. Because 1 + 2 > 3, you cannot have a (1, 2, 3) triangle. So (2, 3, 4) is the first triangle in this sequence, but is there a last triangle? What happens to the shapes as we continue on and on down the sequence of triangles? Will they all be obtuse-angled from now on or will we get some more acute-angled or right-angled triangles later? What are the sizes of the angles in the triangles? For learners who know the cosine rule, this can be a good opportunity to use it. If they use the formula on the first triangle, they can calculate any of the angles (e.g., the one at the top; call it θ) by working out cos θ = (2² + 3² - 4²)/(2 x 2 x 3) = - ¼ so θ = 104.5°, correct to 1 decimal place. Because each triangle has sides of consecutive integer length, it is possible to find a general formula. Writing the side lengths as x, x + 1 and x + 2, and using the cosine rule, taking θ as the angle opposite the largest (x + 2) side, gives, cos θ = (x-3)/2x for x > 1. (Alternatively, you could label the sides (x – 1), x and (x + 1).) Some values for (x-3)/2x and the angle θ are given in the table below.
| 2 | - ¼ | 104.5 |
| 3 | 0 | 90 |
| 4 | ⅛ | 82.80 |
| 5 | ⅕ | 78.5 |
| 6 | ¼ | 75.5 |
| 7 | 2/7 | 73.4 |
| 8 | 5/16 | 71.8 |
| 9 | ⅓ | 70.5 |
| 10 | 7/20 | 69.5 |
The change of the cosine from negative to positive results in a change in θ from greater than 90° to less than 90°.
SUMMARY
You could conclude the lesson with a plenary in which learners talk about what they have found out about the sequence of triangles. It would be interesting to probe learners’ thoughts on what will happen to these shapes if they continue growing in this way forever. How will the shape of the triangles change as x increases?
HOME LEARNING
Learners could make a poster to summarise what they have found out about this triangle sequence. Alternatively, they could explore a different triangle sequence, such as where the sides are of the form 2x, 3x, 4x – multiplying rather than adding. This is much easier, because all of the triangles are mathematically similar.









