It can be difficult to find problem-solving tasks that are suitable for Key Stage 3 students and which focus on central areas of the curriculum. Good problem-solving tasks can sometimes take a great deal of time to do well, which might be hard to justify in the busy scheme of work. This standalone lesson is based on the scenario of a teacher buying doughnuts for each student in their class (whether you wish to buy real doughnuts for your students is up to you!) The doughnuts are all identical but come in two different-sized bags, which cost different amounts of money. What total numbers of doughnuts is it possible to buy and what is the cheapest way of getting at least a certain total number of doughnuts? Exploring these questions involves students in considering multiples and systematically examining various combinations of the bags. Justifying their findings requires and develops careful mathematical reasoning. Some of the conclusions may be surprising, such as that it is sometimes cheaper to buy more doughnuts! Investigating when and why this happens provides a good challenge for students that helps them to use what they know and apply it to an unfamiliar context.
Starter activity
Draw this table on the board. 
Q. In a shop you can buy doughnuts in small bags or large bags. The doughnuts are all the same, but you get 4 in a small bag and 7 in a large bag. Is it possible to buy exactly 15 doughnuts? You can’t split bags! If you can’t do it, say why not. If you can do it, say how, and whether you can do it in more than one way. Students could think about this question in pairs. Give them time to experiment on paper . The only way to get exactly 15 doughnuts is to buy 2 small bags and 1 large bag. Q. What other numbers of doughnuts can you get using these bags? What numbers can’t you get? Why? We assume that the shop has an unlimited number of both kinds of bag. Students will probably realise straightaway that you can’t get 1, 2 or 3 doughnuts, since the smallest bag contains 4. It is also probably obvious that you can’t get 5 or 6 doughnuts. Further exploration will need to be systematic, either beginning with specific target numbers and trying to work out how to make them, or starting with different combinations of the bags (perhaps in a two-way table) and seeing what totals they produce. A complete list of the impossible numbers of doughnuts is: 1, 2, 3, 5, 6, 9, 10, 13 and 17, so there are 9 impossible numbers. One way to see that all numbers
above 17 are going to be possible is to write them out in four columns: 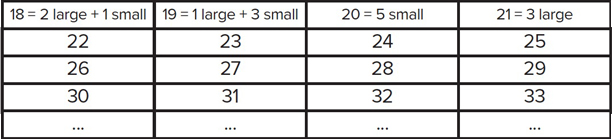
We can do the first row (18, 19, 20, 21), as shown. Each number in the second row is 4 more than the number above it in the first row, so we must be able to do each of these numbers by adding 1 small bag to the collection we have immediately above it in the top row. Similarly, each subsequent row is going to be possible by adding a small bag to the number above it. This means that all numbers from 18 must be possible. (This is an example of a proof by induction.) Main activity Q. Here is some more information about the bags of doughnuts. 
Q. What do you think would be a sensible price to go where the question marks are? Why? Students could reason that 7 is just less than double 4, so the price should be a little less than double £1. They might use ratio to work out that the missing price should be £1.75, but this assumes that the cost per doughnut is the same for a small bag and a large bag. This is unlikely, since there is usually a discount for buying more. So a more reasonable figure would be something like £1.50. Q. Let’s agree that a large bag of doughnuts costs £1.50. If there are 31 students in the class, and I need one doughnut for each student, what is the cheapest way to get enough doughnuts? You could vary the target number according to how many students are in your class today (even if not everyone likes doughnuts!), and either include yourself or not, in order to make the number more interesting. Now we don’t have to have exactly the right number of doughnuts – if some are left over, that is all right – but we want to spend as little money as possible. Q. What happens with different numbers of students in the class? Is it ever cheaper to buy more doughnuts? Students could work on these questions in groups and explore the possibilities.
You could conclude the lesson with a plenary in which the students talk about what they have found out and learned. They might have thought about the fact that the price per doughnut is less for the large bag, so it is a good strategy to try to use as many large bags as possible. If the target number is a multiple of 7 (the number of doughnuts in a large bag), then using just large bags must be optimal. If the target number is a multiple of 4 (the number of doughnuts in a small bag), then using just small bags may be optimal (e.g., for making 8 doughnuts), but it isn’t necessarily. For example, if you need 20 doughnuts, you could use 5 small bags, which would cost £5, but 3 large bags would give you 21 doughnuts and cost only £4.50, so this is an example of where buying more doughnuts costs you less! For your £5 you could get a maximum of 22 doughnuts, by buying 2 large bags and 2 small bags. The only way to get exactly 31 doughnuts is to buy 1 large bag and 6 small bags, costing £7.50, but this is not the cheapest way to get at least 31 doughnuts. It is actually cheaper to buy 32 doughnuts. Students might think that the only way to get 32 doughnuts is to buy 8 small bags, which would cost £8, but in fact there is another way. If you buy 4 large bags and 1 small bag, you get 32 doughnuts and it costs only £7, which is cheaper than buying only 31 doughnuts! Students might comment on aspects of this problem which are less true to real life. Maybe not every student will want a doughnut, or someone might be absent. The doughnuts in the two sizes of bags might not be identical – one size of bag might contain fresher doughnuts than the other, or the flavours might differ. Also, if you are buying so many doughnuts you might be able to arrange a deal with the shopkeeper. It is good if students think about the assumptions and limitations within real-life scenarios.
For a huge selection of free maths lesson plans for KS3 and KS4 click here.








