Learning mathematics is about making sense of mathematical situations. These puzzles provide an interesting context in which students can make predictions and conjectures and develop their powers of mathematical reasoning, says Colin Foster…
Today you will…
- Investigate the relationship between numbers in a diagram and justify your reasoning
Often in mathematics lessons KS3 students are presented with lots of short closed questions to tackle, one after the other, where the reasoning length in each question is just one step. By contrast, in this lesson students are invited to explore one bigger problem for the whole lesson.
Arithmagons (also known as addagons) are polygons with a circle number placed at each vertex and a square number on each side so that each square number is the sum of the two adjacent circle numbers. Finding the missing square numbers in a triangular arithmagon when the circle numbers are given just involves addition, but finding the square numbers when the circle numbers are given is much more challenging. Although the problem is equivalent to solving three simultaneous linear equations in three unknowns, it is not necessary for students to use algebra to make sense of the structure. Some careful reasoning enables them to solve the general problem and see why it will always work. However, an algebraic approach offers considerable benefits when working with arithmagons with more than three vertices, which some students might explore towards the end of the lesson.
Starter activity
Have the diagram below on the board at the start of the lesson
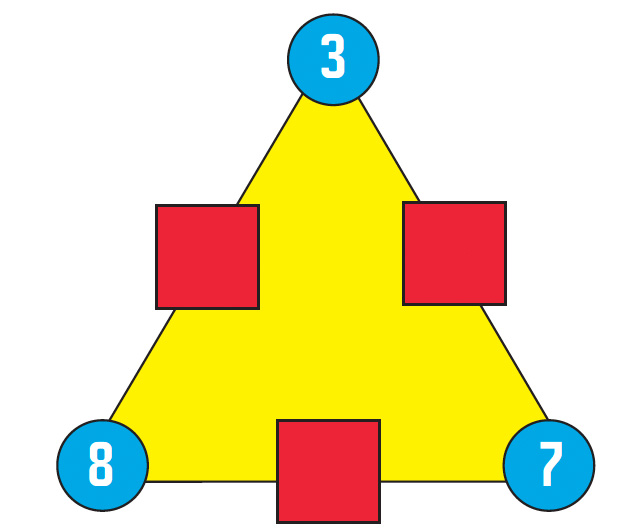
Q Watch what I do. You might have seen this before – that’s OK – we can do new things with it.
Fill in the box numbers as below, saying:
Q. 3 plus 8 is 11, 8 plus 7 is 15, 3 plus 7 is 10.
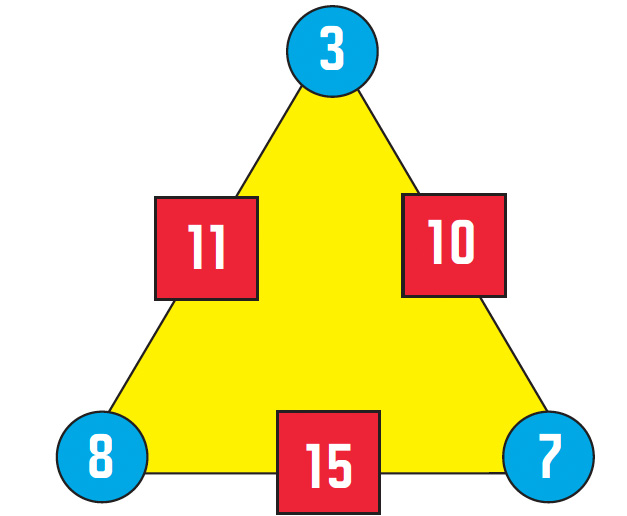
Give students a moment to take in what you have done and then leave the completed diagram on the board for them to look back to later.
Q. Now here are four for you to try. Can you find the missing numbers? Each time the square number is the sum of the circle numbers on either side of it.
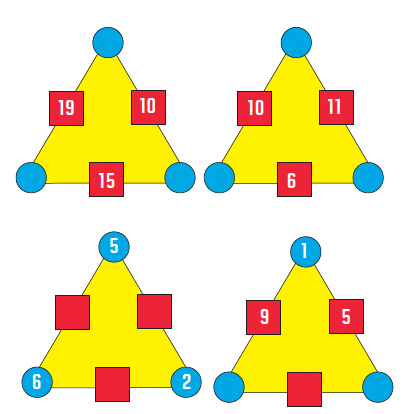
Give students a few minutes to work on these. The first one should be straightforward, the second involves subtraction and the third and fourth are more difficult. The answers, in order, are {11, 7, 8}, {8, 12, 4}, {7, 12, 3} and {7.5, 2.5, 3.5}. The last one may be particularly challenging, given the halves in the answers. If no one can do it at the moment, you could leave it up on the board as a challenge for later, rather than spoiling it by giving the answer.
Main Activities
These diagrams are called arithmagons. What have you learned about them from what you have done so far? When are they easy and when are they hard?
Students will notice that if you are given the circle numbers it is quite easy to work out the square numbers, but starting with the square numbers and working out the circle numbers is much harder! Arithmagons are also easier to do if all of the numbers are small positive integers.
If I just give you the three square numbers, can you always find the circle numbers? What other questions can you ask about arithmagons?
Students might wonder whether there is always just one possible set of three circle numbers for any given three square numbers. Might there sometimes be more than one? Might there sometimes be no possible circle numbers that will work?
There is lots here for students to investigate and they will need plenty of time to explore the possibilities. Encourage students to begin by trying specific numbers and recording carefully what they have done. Encourage them to notice what happens when they change the numbers and to try to explain their findings. When testing out their conjectures, one student could invent three circle numbers, work out the square numbers (carefully!), and then give just the square numbers to the person next to them to see if they can recreate the original circle numbers.
Home learning
Students could try out the arithmagon puzzle on their parents/carers and see if they can find the circle numbers given the three square numbers! Can the student then explain to them how to find the circle numbers and why it works?
Summary
You could conclude the lesson with a plenary in which the students talk about what they have found out. They may notice patterns to do with odd and even numbers and interesting results, such as that the sum of the square numbers is always twice the sum of the circle numbers. This makes sense, because each circle number is counted twice by contributing to two different square numbers. Students could try to explain this carefully, perhaps with a diagram showing why it will always work.
This is a useful result, because one way to solve an arithmagon in which you are given just the three square numbers is to start by adding these together and halving the answer, to give you the total of the three circle numbers. You can write this in the middle of the arithmagon. For example, for the arithmagon shown below, the total of the square numbers is 19 + 10 + 15 = 44, so the circle total is 22 (shown in green at the centre).
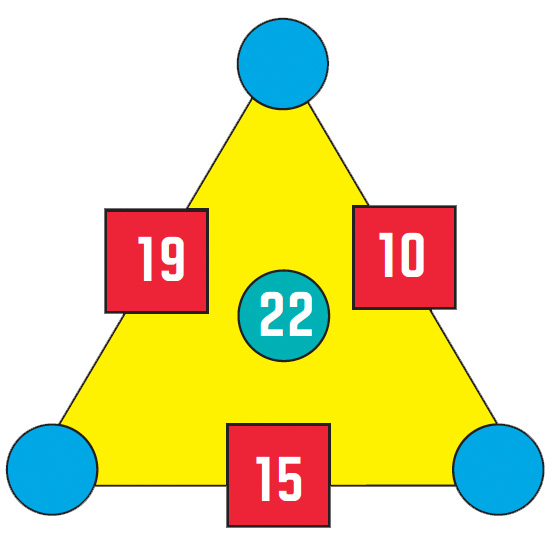
If we now focus on the bottom square number, for instance, this tells us that the bottom two circles add up to 15. Since we know that all three circles add up to 22, we know that the top circle must be 22 – 15 = 7.
We could use the same process to find the values for the other two circles, but we don’t need to, since once we have one circle it is easy to work out the values of the other circles by subtracting from the squares adjacent to them. This gives the circle values of 7, 12 and 3.
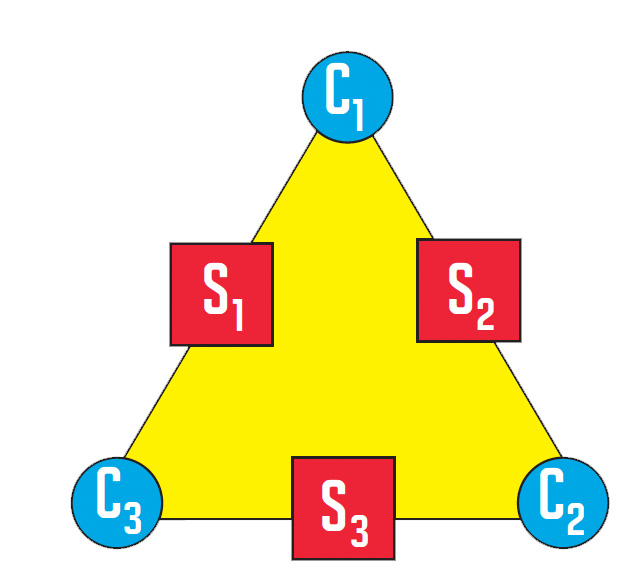
The same process could be represented more formally by labelling the six numbers as in the diagram below and writing and solving the three equations:
c1 + c2 = s2
c1 + c3 = s1
c2 + c3 = s3
(If you use this notation, make sure that students understand that the subscript numbers are just labels for which c-number or s-number we are referring to, and not indices.)
About our expert
Colin Foster is a Senior Research Fellow in mathematics education in the School of Education at the University of Nottingham. He has written many books and articles for mathematics teachers (see www.foster77.co.uk).
Additional resources
A good website for playing around with the numbers in an arithmagon is http://nrich.maths.org/2670. the page http://nrich.maths.org/7447 extends this to ‘multiplication arithmagons’, and http://flashmaths.co.uk/viewflash.php?i d=24 offers both in one.
Stretch them further
What happens if you make a square arithmagon, with four circle numbers and four square numbers? things work out very differently this time! what happens with arithmagons with five or more vertices?
For a huge selection of free maths lesson plans for KS3 and KS4 click here.











Learning mathematics is about making sense of mathematical situations. These puzzles provide an interesting context in which students can make predictions and conjectures and develop their powers…